Gradient descent — mathematical explanation & full derivation

Machine learning Mathematics in Machine Learning

Posted by admin on 2025-09-19 21:24:48 | Last Updated by tintin_2003 on 2025-10-16 04:50:42

Share: Facebook | Twitter | Whatsapp | Linkedin Visits: 90

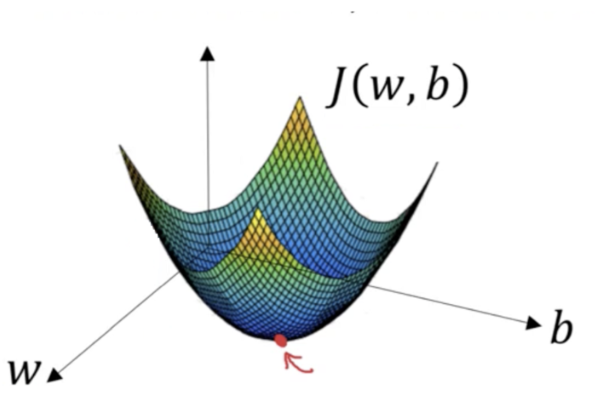
Gradient descent — mathematical explanation & full derivation

Gradient Descent: Mathematical Proof and Code Implementation

Mathematical Foundation

1. Basic Setup and Definitions

Let f(x) be a differentiable function we want to minimize, where x ∈ R^n.

Goal: Find x* such that f(x*) = min f(x)

Key Insight: The gradient ∇f(x) points in the direction of steepest ascent.
Therefore, -∇f(x) points in the direction of steepest descent.

2. The Gradient Descent Algorithm

Update Rule: x_{k+1} = x_k - α∇f(x_k)

Where:
- x_k is the current point at iteration k
- α > 0 is the learning rate (step size)  
- ∇f(x_k) is the gradient at x_k

3. Mathematical Proof of Convergence

Assumptions:

1. f is continuously differentiable
2. f has Lipschitz continuous gradient with constant L > 0:
   ||∇f(x) - ∇f(y)|| ≤ L||x - y|| for all x, y
3. f is bounded below: f(x) ≥ f* for all x  
4. Learning rate satisfies: 0 < α < 2/L

Proof:

Step 1: Show that the function value decreases at each iteration

Using Taylor expansion around x_k:

f(x_{k+1}) = f(x_k - α∇f(x_k))
           ≤ f(x_k) + ∇f(x_k)^T(-α∇f(x_k)) + (L/2)||(-α∇f(x_k))||²
           = f(x_k) - α||∇f(x_k)||² + (Lα²/2)||∇f(x_k)||²
           = f(x_k) - α(1 - Lα/2)||∇f(x_k)||²

Since 0 < α < 2/L, we have (1 - Lα/2) > 0, so:

f(x_{k+1}) ≤ f(x_k) - α(1 - Lα/2)||∇f(x_k)||²

Step 2: Show convergence of gradient to zero

Rearranging the inequality:
α(1 - Lα/2)||∇f(x_k)||² ≤ f(x_k) - f(x_{k+1})

Summing from k = 0 to K-1:
α(1 - Lα/2) Σ(k=0 to K-1) ||∇f(x_k)||² ≤ f(x_0) - f(x_K)

Since f is bounded below:
α(1 - Lα/2) Σ(k=0 to K-1) ||∇f(x_k)||² ≤ f(x_0) - f* < ∞

This implies: Σ ||∇f(x_k)||² < ∞
Therefore: ||∇f(x_k)|| → 0 as k → ∞

Step 3: Convergence rates

For convex functions:
f(x_k) - f* ≤ ||x_0 - x*||² / (2αk)
This gives O(1/k) convergence rate.

For strongly convex functions with parameter μ > 0:
||x_k - x*||² ≤ ((L-μ)/(L+μ))^k ||x_0 - x*||²
This gives exponential (linear) convergence.

4. Why the Proof Works

The mathematical proof establishes three crucial results:

  1. Monotonic Decrease: Each iteration reduces the function value
  2. Gradient Convergence: The gradient approaches zero
  3. Convergence Rate: Quantifies how fast we reach the minimum

Code Implementation

Basic Gradient Descent Implementation

import numpy as np
import matplotlib.pyplot as plt

def gradient_descent(f, grad_f, x0, alpha=0.01, max_iter=1000, tol=1e-6):
    """
    Gradient descent optimization algorithm
    
    Args:
        f: objective function to minimize
        grad_f: gradient of the objective function
        x0: initial point
        alpha: learning rate
        max_iter: maximum iterations
        tol: tolerance for convergence
    
    Returns:
        x: optimal point
        history: optimization history
    """
    x = x0.copy()
    history = {'x': [x.copy()], 'f': [f(x)], 'grad_norm': []}
    
    for i in range(max_iter):
        grad = grad_f(x)
        grad_norm = np.linalg.norm(grad)
        history['grad_norm'].append(grad_norm)
        
        # Check convergence
        if grad_norm < tol:
            print(f"Converged after {i} iterations")
            break
            
        # Update step
        x = x - alpha * grad
        
        # Store history
        history['x'].append(x.copy())
        history['f'].append(f(x))
    
    return x, history

# Example 1: Quadratic function f(x) = x^2 + 2x + 1
def f1(x):
    return x**2 + 2*x + 1

def grad_f1(x):
    return 2*x + 2

# Example 2: Multi-dimensional quadratic
def f2(x):
    return x[0]**2 + 2*x[1]**2 + x[0]*x[1] + x[0] + 2*x[1]

def grad_f2(x):
    return np.array([2*x[0] + x[1] + 1, 4*x[1] + x[0] + 2])

# Test 1D optimization
print("1D Optimization:")
x0 = np.array([5.0])
x_opt, hist = gradient_descent(f1, grad_f1, x0, alpha=0.1)
print(f"Optimal x: {x_opt[0]:.6f}")
print(f"Optimal f(x): {f1(x_opt):.6f}")
print(f"Theoretical minimum: x = -1, f(x) = 0")

# Test 2D optimization  
print("\n2D Optimization:")
x0 = np.array([3.0, 2.0])
x_opt, hist = gradient_descent(f2, grad_f2, x0, alpha=0.1)
print(f"Optimal x: [{x_opt[0]:.6f}, {x_opt[1]:.6f}]")
print(f"Optimal f(x): {f2(x_opt):.6f}")

Visualization Code

def visualize_convergence(history, title="Gradient Descent Convergence"):
    """Visualize the convergence of gradient descent"""
    fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))
    
    # Plot function value over iterations
    ax1.plot(history['f'])
    ax1.set_xlabel('Iteration')
    ax1.set_ylabel('Function Value')
    ax1.set_title('Function Value Convergence')
    ax1.grid(True)
    
    # Plot gradient norm over iterations
    ax2.plot(history['grad_norm'])
    ax2.set_xlabel('Iteration')
    ax2.set_ylabel('||∇f(x)||')
    ax2.set_title('Gradient Norm Convergence')
    ax2.set_yscale('log')
    ax2.grid(True)
    
    plt.suptitle(title)
    plt.tight_layout()
    plt.show()

# Visualize the optimization process
visualize_convergence(hist, "2D Quadratic Function Optimization")

Advanced Implementation with Adaptive Learning Rate

def gradient_descent_adaptive(f, grad_f, x0, alpha_init=0.1, beta=0.5, 
                            max_iter=1000, tol=1e-6):
    """
    Gradient descent with backtracking line search
    
    Implements the Armijo condition for adaptive step size
    """
    x = x0.copy()
    alpha = alpha_init
    c1 = 1e-4  # Armijo parameter
    history = {'x': [x.copy()], 'f': [f(x)], 'alpha': [alpha]}
    
    for i in range(max_iter):
        grad = grad_f(x)
        
        if np.linalg.norm(grad) < tol:
            print(f"Converged after {i} iterations")
            break
        
        # Backtracking line search
        alpha = alpha_init
        fx = f(x)
        
        while True:
            x_new = x - alpha * grad
            fx_new = f(x_new)
            
            # Armijo condition
            if fx_new <= fx - c1 * alpha * np.dot(grad, grad):
                break
            alpha *= beta
            
            if alpha < 1e-10:
                print("Line search failed")
                break
        
        x = x_new
        history['x'].append(x.copy())
        history['f'].append(fx_new)
        history['alpha'].append(alpha)
    
    return x, history

# Test adaptive version
print("\nAdaptive Learning Rate:")
x0 = np.array([3.0, 2.0])
x_opt_adaptive, hist_adaptive = gradient_descent_adaptive(f2, grad_f2, x0)
print(f"Optimal x: [{x_opt_adaptive[0]:.6f}, {x_opt_adaptive[1]:.6f}]")
print(f"Final learning rate: {hist_adaptive['alpha'][-1]:.6f}")

Convergence Analysis Code

def analyze_convergence_rate(history, theoretical_rate=None):
    """Analyze the convergence rate of gradient descent"""
    f_vals = np.array(history['f'])
    f_min = f_vals[-1]  # Assume last value is close to minimum
    
    # Calculate convergence error
    error = f_vals - f_min
    error = error[error > 0]  # Remove non-positive values
    
    if len(error) < 10:
        print("Not enough data for convergence analysis")
        return
    
    # Fit exponential decay: error ≈ C * r^k
    log_error = np.log(error)
    iterations = np.arange(len(log_error))
    
    # Linear regression in log space
    coeffs = np.polyfit(iterations, log_error, 1)
    convergence_rate = np.exp(coeffs[0])
    
    print(f"Empirical convergence rate: {convergence_rate:.4f}")
    if theoretical_rate:
        print(f"Theoretical rate: {theoretical_rate:.4f}")
    
    # Plot convergence analysis
    plt.figure(figsize=(10, 6))
    plt.semilogy(error, 'b-', label='Actual Error')
    plt.semilogy(np.exp(coeffs[1]) * convergence_rate**iterations, 'r--', 
                label=f'Fitted: {convergence_rate:.4f}^k')
    plt.xlabel('Iteration')
    plt.ylabel('Error (log scale)')
    plt.title('Convergence Rate Analysis')
    plt.legend()
    plt.grid(True)
    plt.show()

# Analyze convergence for our example
analyze_convergence_rate(hist)

Key Insights from the Proof

  1. Learning Rate Bounds: The proof shows α must be less than 2/L for convergence
  2. Gradient Vanishing: The gradient norm must approach zero for convergence
  3. Function Decrease: Each step guarantees a decrease in function value
  4. Rate Dependence: Convergence rate depends on function properties (convexity, strong convexity)

The mathematical proof provides the theoretical foundation, while the code demonstrates these principles in practice, showing how the algorithm behaves and converges to optimal solutions.

Search
Categories
Recent Articles
Popular News
Leave a Comment: