Derivation of the Softmax Function

Posted by admin on 2025-09-18 15:59:15 | Last Updated by tintin_2003 on 2025-10-16 04:53:41

Share: Facebook | Twitter | Whatsapp | Linkedin Visits: 31

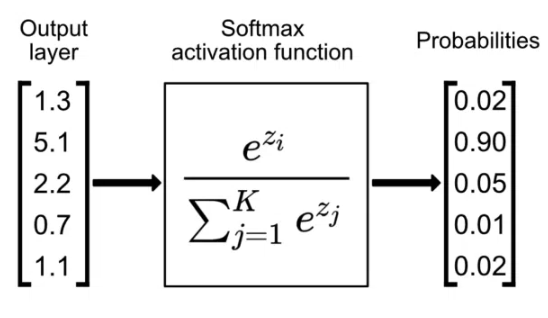
Problem Setup

Suppose we have a vector of raw scores (logits) z = [z₁, z₂, ..., zₖ] and we want to convert these into a probability distribution over k classes. We need a function that satisfies:

1. All outputs are positive: p(yᵢ) > 0
2. All outputs sum to 1: Σᵢ p(yᵢ) = 1
3. Larger inputs should correspond to larger probabilities (monotonic)

Derivation

Step 1: Exponential Transformation

To ensure all outputs are positive, we apply the exponential function:

exp(zᵢ)

Since exp(x) > 0 for all real x, this satisfies our first requirement.

Step 2: Normalization

To ensure the outputs sum to 1, we normalize by the sum of all exponentials:

p(yᵢ) = exp(zᵢ) / Σⱼ₌₁ᵏ exp(zⱼ)

Let's verify this sums to 1:

Σᵢ₌₁ᵏ p(yᵢ) = Σᵢ₌₁ᵏ [exp(zᵢ) / Σⱼ₌₁ᵏ exp(zⱼ)]
              = [Σᵢ₌₁ᵏ exp(zᵢ)] / [Σⱼ₌₁ᵏ exp(zⱼ)]
              = 1 ✓

Step 3: Final Softmax Expression

This gives us the softmax function:

softmax(zᵢ) = exp(zᵢ) / Σⱼ₌₁ᵏ exp(zⱼ)

Or in vector notation:

softmax(z) = exp(z) / ||exp(z)||₁

where ||·||₁ denotes the L1 norm (sum of absolute values).

Properties

The derived softmax function has several important properties:

1. Probability distribution: 0 < softmax(zᵢ) < 1 and Σᵢ softmax(zᵢ) = 1

2. Translation invariance: softmax(z + c) = softmax(z) for any constant c

   • This means subtracting the maximum value for numerical stability doesn't change the result

3. Smooth approximation to argmax: As temperature → 0, softmax approaches a one-hot vector at the maximum element

4. Differentiable: Unlike the argmax function, softmax is everywhere differentiable, making it suitable for gradient-based optimization

Numerical Stability

In practice, we often implement softmax as:

softmax(zᵢ) = exp(zᵢ - max(z)) / Σⱼ exp(zⱼ - max(z))

This prevents numerical overflow while maintaining the same mathematical result due to translation invariance.

The softmax function thus provides an elegant solution for converting arbitrary real-valued scores into valid probability distributions, which is why it's ubiquitous in classification tasks and attention mechanisms in machine learning.

Softmax Function: Mathematical Derivation with Code

Problem Setup

In machine learning, we often need to convert raw scores (logits) into probabilities. Given a vector z = [z₁, z₂, ..., zₖ], we need a function that:

1. Positivity: All outputs are positive → p(yᵢ) > 0
2. Normalization: Outputs sum to 1 → Σᵢ p(yᵢ) = 1
3. Monotonicity: Larger inputs → larger probabilities

import numpy as np
import matplotlib.pyplot as plt

# Example: Raw scores from a neural network
raw_scores = np.array([2.0, 1.0, 0.1])
print(f"Raw scores: {raw_scores}")
print(f"Sum: {np.sum(raw_scores)} (not a valid probability distribution)")

Step-by-Step Derivation

Step 1: Exponential Transformation

To ensure positivity, apply the exponential function:

Mathematical form: exp(zᵢ)

def step1_exponential(z):
    """Apply exponential to ensure positivity"""
    return np.exp(z)

exp_scores = step1_exponential(raw_scores)
print(f"After exp(): {exp_scores}")
print(f"All positive? {np.all(exp_scores > 0)}")
print(f"Sum: {np.sum(exp_scores)} (still not normalized)")

Step 2: Normalization

To ensure the outputs sum to 1, divide by the sum of all exponentials:

Mathematical form: p(yᵢ) = exp(zᵢ) / Σⱼ₌₁ᵏ exp(zⱼ)

def step2_normalization(z):
    """Apply exponential and normalize"""
    exp_z = np.exp(z)
    return exp_z / np.sum(exp_z)

probabilities = step2_normalization(raw_scores)
print(f"Probabilities: {probabilities}")
print(f"Sum: {np.sum(probabilities)} (valid probability distribution!)")

Step 3: Final Softmax Expression

This gives us the complete softmax function:

Mathematical form:

softmax(zᵢ) = exp(zᵢ) / Σⱼ₌₁ᵏ exp(zⱼ)

Vector notation:

softmax(z) = exp(z) / ||exp(z)||₁

def softmax_basic(z):
    """Basic softmax implementation"""
    exp_z = np.exp(z)
    return exp_z / np.sum(exp_z)

# Test the function
result = softmax_basic(raw_scores)
print(f"Softmax result: {result}")
print(f"Verification - Sum: {np.sum(result):.10f}")

Numerical Stability Issues

The basic implementation can cause numerical overflow:

# Problematic case: large numbers
large_scores = np.array([1000, 1001, 1002])
print(f"Large scores: {large_scores}")

try:
    result = softmax_basic(large_scores)
    print(f"Result: {result}")
except:
    # This will likely produce NaN due to overflow
    exp_large = np.exp(large_scores)
    print(f"exp(large_scores): {exp_large}")  # Will be inf

Solution: Translation Invariance

Key Property: softmax(z + c) = softmax(z) for any constant c

Proof:

softmax(zᵢ + c) = exp(zᵢ + c) / Σⱼ exp(zⱼ + c)
                = exp(zᵢ)exp(c) / [exp(c) Σⱼ exp(zⱼ)]
                = exp(zᵢ) / Σⱼ exp(zⱼ)
                = softmax(zᵢ)

def softmax_stable(z):
    """Numerically stable softmax implementation"""
    # Subtract maximum to prevent overflow
    z_shifted = z - np.max(z)
    exp_z = np.exp(z_shifted)
    return exp_z / np.sum(exp_z)

# Test with large numbers
result_stable = softmax_stable(large_scores)
print(f"Stable softmax result: {result_stable}")
print(f"Sum: {np.sum(result_stable)}")

# Verify translation invariance
original = softmax_stable([1, 2, 3])
shifted = softmax_stable([101, 102, 103])  # Added 100 to each
print(f"Original: {original}")
print(f"Shifted:  {shifted}")
print(f"Equal? {np.allclose(original, shifted)}")

Properties and Verification

1. Probability Distribution

def verify_probability_distribution(z):
    """Verify softmax produces valid probabilities"""
    probs = softmax_stable(z)
    
    # Check all positive
    all_positive = np.all(probs > 0)
    
    # Check sum to 1
    sums_to_one = np.isclose(np.sum(probs), 1.0)
    
    # Check between 0 and 1
    in_range = np.all((probs >= 0) & (probs <= 1))
    
    return all_positive, sums_to_one, in_range, probs

test_vectors = [
    [1, 2, 3],
    [-5, 0, 5],
    [100, 200, 300],
    [0.1, 0.1, 0.1]
]

for z in test_vectors:
    pos, sum_one, in_range, probs = verify_probability_distribution(z)
    print(f"z={z}: positive={pos}, sum=1={sum_one}, in_range={in_range}")

2. Temperature Parameter

def softmax_with_temperature(z, temperature=1.0):
    """Softmax with temperature parameter"""
    z_temp = np.array(z) / temperature
    return softmax_stable(z_temp)

# Demonstrate effect of temperature
z = [1, 2, 5]
temperatures = [0.1, 0.5, 1.0, 2.0, 10.0]

print("Effect of temperature on softmax:")
print(f"Input: {z}")
for T in temperatures:
    probs = softmax_with_temperature(z, T)
    print(f"T={T:4.1f}: {probs}")

3. Gradient (for backpropagation)

def softmax_gradient(z, i):
    """Compute gradient of softmax w.r.t. input z_i"""
    s = softmax_stable(z)
    # Gradient: s_i(δ_ij - s_j) where δ_ij is Kronecker delta
    n = len(z)
    grad = np.zeros(n)
    for j in range(n):
        if i == j:
            grad[j] = s[i] * (1 - s[j])  # δ_ij = 1
        else:
            grad[j] = -s[i] * s[j]       # δ_ij = 0
    return grad

# Example gradient computation
z = [1, 2, 3]
for i in range(len(z)):
    grad = softmax_gradient(z, i)
    print(f"∇softmax(z)_{i} = {grad}")

Complete Implementation with Documentation

class Softmax:
    """
    Numerically stable softmax implementation with utilities
    """
    
    @staticmethod
    def forward(z, temperature=1.0):
        """
        Compute softmax probabilities
        
        Args:
            z: Input logits (array-like)
            temperature: Temperature parameter (default: 1.0)
            
        Returns:
            numpy.ndarray: Softmax probabilities
        """
        z = np.array(z) / temperature
        z_shifted = z - np.max(z)  # Numerical stability
        exp_z = np.exp(z_shifted)
        return exp_z / np.sum(exp_z)
    
    @staticmethod
    def log_softmax(z, temperature=1.0):
        """
        Compute log-softmax (more numerically stable for loss computation)
        
        Args:
            z: Input logits (array-like)
            temperature: Temperature parameter (default: 1.0)
            
        Returns:
            numpy.ndarray: Log probabilities
        """
        z = np.array(z) / temperature
        z_shifted = z - np.max(z)
        log_sum_exp = np.log(np.sum(np.exp(z_shifted)))
        return z_shifted - log_sum_exp
    
    @staticmethod
    def cross_entropy_loss(logits, targets):
        """
        Compute cross-entropy loss using numerically stable log-softmax
        
        Args:
            logits: Raw scores from model
            targets: True class indices or one-hot vectors
            
        Returns:
            float: Cross-entropy loss
        """
        log_probs = Softmax.log_softmax(logits)
        
        if targets.ndim == 1:  # Class indices
            return -log_probs[targets]
        else:  # One-hot vectors
            return -np.sum(targets * log_probs)

# Demonstration
print("=== Complete Softmax Implementation ===")
logits = [2.0, 1.0, 0.1]
probs = Softmax.forward(logits)
log_probs = Softmax.log_softmax(logits)

print(f"Logits: {logits}")
print(f"Probabilities: {probs}")
print(f"Log probabilities: {log_probs}")
print(f"Verification - exp(log_probs): {np.exp(log_probs)}")

Applications in Machine Learning

1. Multi-class Classification

# Example: 3-class classification
def neural_network_example():
    """Simulate a neural network's final layer"""
    # Simulate raw outputs from final layer
    logits = np.array([2.1, 0.5, 1.8])  # Scores for classes 0, 1, 2
    
    # Convert to probabilities
    probs = Softmax.forward(logits)
    predicted_class = np.argmax(probs)
    confidence = probs[predicted_class]
    
    print(f"Raw logits: {logits}")
    print(f"Probabilities: {probs}")
    print(f"Predicted class: {predicted_class}")
    print(f"Confidence: {confidence:.3f}")
    
    return probs

neural_network_example()

2. Attention Mechanisms

def attention_example():
    """Softmax in attention mechanism"""
    # Attention scores (query-key similarities)
    attention_scores = np.array([0.8, 1.2, 0.3, 2.1, 0.9])
    
    # Convert to attention weights
    attention_weights = Softmax.forward(attention_scores)
    
    # Values to attend to
    values = np.array([
        [1, 2, 3],    # Value vector 1
        [4, 5, 6],    # Value vector 2  
        [7, 8, 9],    # Value vector 3
        [10, 11, 12], # Value vector 4
        [13, 14, 15]  # Value vector 5
    ])
    
    # Weighted combination
    attended_output = np.sum(attention_weights.reshape(-1, 1) * values, axis=0)
    
    print("Attention Mechanism Example:")
    print(f"Attention scores: {attention_scores}")
    print(f"Attention weights: {attention_weights}")
    print(f"Attended output: {attended_output}")

attention_example()

Summary

The softmax function elegantly solves the problem of converting arbitrary real-valued scores into valid probability distributions. Key takeaways:

1. Mathematical elegance: Natural combination of exponential (for positivity) and normalization
2. Numerical stability: Always subtract maximum value before computing
3. Differentiability: Smooth gradients enable gradient-based optimization
4. Versatility: Used in classification, attention, and many other ML applications

The derivation shows how mathematical constraints (positivity, normalization, monotonicity) naturally lead to the exponential and normalization steps that define softmax.